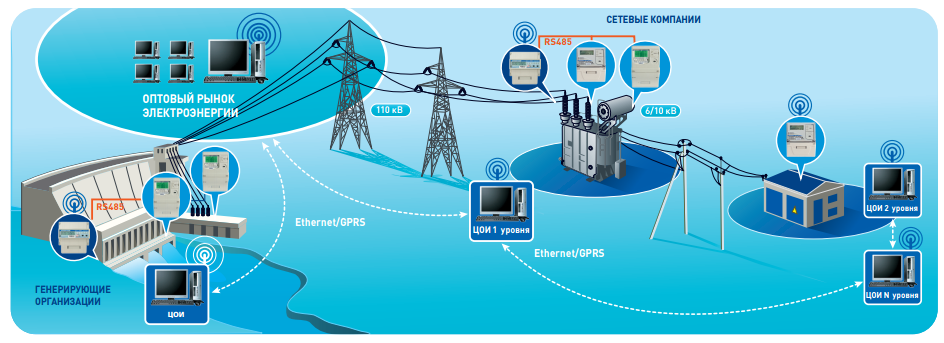
В  связи с созданием системы коммерческого учета оптового  рынка электрической  энергии  и  организацией централизованного сбора данных с помощью интегрированной автоматизированной системы НП «АТС» некоторыми специалистами в качестве одной из самых актуальных  проблем  выдвигается  проблема сбалансированности значений учетных показателей (данных учета) между собой по рынку в целом, его энергозонам и даже по отдельным сетевым элементам (рис. 1). Эта проблема не нова, ее уже ставили и пытались решать при распределении  газа,  жидких  углеводородов,  то  есть  там, где объем отпуска товара измеряется одними приборами, а объем потребления, служащий в качестве основания для финансовых расчетов, другими.

 Под  условием  сбалансированности  данных  учета понимается определение численных значений учетных показателей,  которые  абсолютно  точно  удовлетворяют составленным балансовым уравнениям. В подавляющем большинстве случаев принимается, что учетные показатели  представляют  собой  детерминированные величины,  их  законы  распределения игнорируются. Номенклатура  учетных  показателей,  вид  балансовых уравнений, а также способы получения значений учетных показателей являются условиями учетной задачи. Решение  учетной  задачи  служит  условием  измерительной задачи. Выявив перечень учетных показателей, необходимо дать ответ на вопрос: как и с какой погрешностью получить их численные значения. Напомним, что результаты решения измерительной задачи всегда выражаются случайными величинами, законы распределения которых обычно описываются с помощью точечных  оценок.  Главным  следствием  этого  факта  является вероятностный характер всех чисел, с которыми имеют дело при коммерческом учете, что влечет за собой обязательный расчет соответствующих погрешностей. Особо следует подчеркнуть, что полученный результат измерения представляет собой не конкретное число, а интервал, внутри которого с некоторой вероятностью Р_д находится  истинное  значение измеряемой  величины. 

 При этом выделение середины интервала – х вовсе не означает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью 1-Р_д даже вне его. Но это «теоретические» результаты. На практике же отсчет по шкале прибора или цифровой код воспринимается  как  истинное  значение величины  и  в  техническом, и, главное, в юридическом смысле. Следствием этого  является, например,  необходимость  хорошо всем известной «подгонки» показаний одного и того же интегрирующего  прибора  на  следующих  друг  за  другом временных интервалах ∆t и на более длительном временном интервале, охватывающем все ∆t.

 Таким образом, при постановке и решении учетной и соответствующих  измерительных задач  имеет  место принципиальное  противоречие,  происходящее  из  различного характера величин, участвующих в абстрактной модели  учетной  задачи  (детерминированные),  и величин, описывающих модель измерений (случайные). Данное противоречие ведет к появлению так называемого «небаланса», то есть невязки балансовых уравнений. Часто о таком небалансе говорят как о «метрологическом». Уменьшение небаланса возможно, в принципе, «метрологическим путем» — уменьшением погрешности с помощью установки более точных средств измерений или введением поправок на известные систематические погрешности. Естественно, что этот небаланс не поддается полной ликвидации с помощью объективных технических (метрологических) методов.

 Если часть значений учетных показателей определяется расчетным путем с использованием модели электрической сети, то, помимо метрологического небаланса (вследствие неточности приборов), имеет место также небаланс,  обусловленный моделированием  сети  при расчетах.  При  этом  исходными  данными  для  расчетов служат чаще всего также результаты измерений.

 Разделение  общего  расчетного  небаланса  на  составляющие (чисто  метрологическую и  связанную  с  погрешностью  моделирования) представляет собой достаточно сложную задачу, не имеющую строгого решения. Проверка выполнения балансовых уравнений путем подстановки в них измеренных и рассчитанных значений физических величин (учетных показателей) на практике служит одним из способов интегрального контроля достоверности этих значений. Для этого необходимо, прежде всего, определить допустимый небаланс, зная границы погрешностей измерений и расчетов значений учетных  показателей  в  реальных условиях  измерений,  и сравнить с ним результат подстановки значений учетных показателей в балансовое уравнение. Такой подход реализован в РД 34.09.10194 и в некоторых других нормативных документах. В общем виде данная задача может ставиться как задача совокупного измерения некоторой величины, представляющей небаланс в i-ом балансовом уравнении

 где D_ij — учетный показатель со своим знаком, N — количество учетных показателей. Априорно принимается,  что  при  правильном  составлении  уравнения  (1) ∆D = 0. В действительности, при подстановке результатов измерений ~ D_ij в (1)

 а  границы  погрешности  определяются  известными методами [1]. Тогда проблема балансировки значений учетных  показателей  формулруется  как  принудительное приравнивание  ∆ ~ D_i нулю в результате корректировки ~ D_ij из (2) по какому-нибудь алгоритму. Разумеется, эта  корректировка не имеет ничего общего с метрологией и является предметом отношений, отражаемых в учетной задаче.

 В коммерческом учете электрической энергии постановка учетных и связанных с ними измерительных задач  зависит  от  правил  работы  рынка.  Кроме  того, проявляются особенности,  связанные  с  технологией электроэнергетического  производства.  Рассмотрим несколько характерных примеров. В  случае,  когда  покупка  и  продажа  электрической энергии происходят в одних и тех же точках электрической  сети  и  в  каждой  точке измерение  производится одним прибором, показание этого прибора естественным образом отображает объемы проданной и купленной  энергии.  Эти  объемы  не  только характеризуются одной и той же физической величиной перетока электрической энергии в заданной точке, но и имеют одинаковое численное значение, полученное из единственного источника  измерительной  информации.  Данная ситуация иллюстрируется рис. 2 при условии, что отчуждение товарной продукции осуществляется в точке 2

 Естественно,  говорить  о  том,  что  был  произведен обмен  товара  «точно»  в количестве  ∆W₂

можно  только условно,  имея  в  виду,  что  действительное  (истинное) значение(в терминах [3])  ∆~W и лежит с некоторой вероятностью внутри интервала, определяемого показаниями  прибора  ∆~W₂ и  известными  границами  погрешностей.

 Однако здесь отсутствует проблема сбалансированности учета: измеренные объемы покупки и продажи совпадают с точностью до погрешности одного и того же прибора. Причем не важно, насколько велика эта погрешность. Значение погрешности, если оно не оговаривается в учетной задаче, влияет на показатели за пределами задачи: например, когда надо сопоставить расход топлива и проданную электрическую энергию и т.п. Если по условиям выполнения измерений, исходя, например, из требований метрологической надежности, в точке 2 на рис. 2 будут установлены два однотипных счетчика (подключенных к одним и тем же ТТ и ТН),  то  возможна  постановка  измерительной  задачи двояким образом.

 • Измерение  величины  приращения  энергии  по показаниям  одного  (заранее выбранного)  прибора.  При  этом  другой  прибор  используется  в целях контроля достоверности и в качестве резервного  при  выходе  из  строя  или  демонтаже основного прибора.

 • Измерение  величины  приращения  энергии  методом неравноточных измерений по показаниям обоих измерительных приборов. Под  неравноточными  измерениями понимается «ряд  измерений  какой-либо  величины,  выполненных различающимися по точности средствами измерений и (или) в разных условиях» [3].  В [4, 5] к ним также относятся измерения, выполненные разными приборами,  различными  исследователями  и  т. д. 

 Измерения приращения  электрической  энергии  двумя  приборами  (счетчиками)  с одинаковыми  классами  точности можно отнести к неравноточным измерениям как предельный случай. В условиях данной учетной и измерительной задачи, как и в предыдущей задаче, проблемы балансировки учетных показателей не возникает. Если между точками поставки участников обращения  электрической  энергии  находятся  сетевые  элементы, принадлежащие  иному  юридическому  лицу (сетевой компании), которое оплачивает потери в этих элементах,  то  с  точки  зрения  балансировки  учетных показателей могут иметь место следующие ситуации.

 1. Все границы собственности на сетевые элементы, принадлежащие сетевой компании, оснащены измерительными приборами, которые, в свою очередь, служат  для  расчетов  за поставленную  и  проданную энергию. Приборы установлены в точках на границах собственности  (балансовой  принадлежности).  Учетным  показателем  сетевой  компании служат  суммарные  технологические  потери  электрической  энергии без их разделения на составляющие. В самом простом случае эта ситуация иллюстрируется рис. 3, где продажа субъектом-продавцом осуществляется в точке 1, а покупка субъектом-покупателем — в точке 2. Такая расстановка средств измерений характеризует  состояние  полной инструментальной  наблюдаемости  всех  учетных  показателей:  проданной  энергии ∆ W1, купленной энергии  ∆W₂ и потерь  δW₁₂. Действительно, если известны результаты измерений  ∆~W₁ и  ∆~W₂, то

 и  балансовое  уравнение,  вытекающее  из  закона сохранения энергии, превращается в очевидное тождество:

 Условием полной инструментальной наблюдаемости является возможность определения всех учетных показателей по результатам прямых измерений, причем  средства  измерений располагаются  точно  на границах владений сетевыми элементами (на границах балансовой принадлежности) субъектов рынка. Данная  ситуация  не  требует  никакой  балансировки значений учетных показателей за исключением  случая, когда потери  δ~W₁₂ становятся отрицательными вследствие своей малости и неблагоприятного соотношения погрешностей измерений  ∆~W₁ и  ∆~W₂ («красные потери»).

 2. Если в условиях ситуации 1 на  рис. 3 один из приборов (например, со стороны 2) отсутствует, то значения  учетных  показателей  потерь  и  потребления  ( δ~W_1′2,∆~W₂′ ) определяются расчетным способом на основании измеренного значения  ∆~W₁ и других режимных параметров, и при их подстановке  в (4) возникает небаланс

 Тогда для принудительного приравнивания нулю  ∆~D в (5)  по условиям балансировки в учетной задаче можно  использовать  корректировку  либо  всех  слагаемых (5),  либо отдельно  выбранного  одного  слагаемого, либо любой выбранной пары слагаемых. Условия корректировки задаются (если на то имеются основания) также в учетной задаче, исходя из каких-то неметрологических правил.

 3. Пусть в условиях полной инструментальной наблюдаемости  обобщенного  учетного показателя  потерь  электрической  энергии  требуется  выделить  его составляющие, каждая из которых не поддается инструментальной наблюдаемости. Например, надо выделить отдельно технические постоянные и нагрузочные  потери  δWT, потери на корону  δWK и потребление на собственные  и  хозяйственные  нужды  подстанций ∆ W_схн. Тогда, подставляя в (4) вместо  δ~W 12 расчетные значения потерь  δWT′ ,  δ WK′ и измеренное потребление ∆~W_схн, получим величину небаланса

 К рассматриваемой ситуации можно отнести и учетную задачу по определению значений учетных показателей (потребления) сетевой компании по заданным группам точек поставки (ГТП) в условиях покупки потерь, не учтенных в узловых ценах. Здесь полностью инструментально наблюдаемы общие потери сетевой компании, с которыми  необходимо сбалансировать  различные  составляющие потребления (потерь), выделяемые в целях оформления финансовых обязательств компании. В зависимости от условий учетной задачи балансировку можно вести по всем составляющим (6) или по группам слагаемых. Можно также «сузить» условия балансировки  и  добиться  нулевого  небаланса  путем строгого выполнения равенства  коррекцией составляющих технологических потерь.

Известная позиция некоторых специалистов и в целом НП «АТС» состоит в том, что весь небаланс  ∆~D в (6) носит «метрологический» характер и он должен быть искусственно приравнен нулю путем изменения значений измеряемых величин  ∆~W₁,  ∆~W₂,  ∆~W_схн. Причем, для привлечения к этому процессу метрологии   ∆~D предлагается  разносить между  результатами  измерений  прямо пропорционально  их  погрешностям,  но  так, чтобы  новые скорректированные значения измеряемых величин не выходили за расчетные границы погрешностей. Кроме того, в учетной задаче в явном виде задано второе условие балансировки  —  разнесение  ∆~D  пропорционально так называемому «коэффициенту качества системы».

 Последний отражает субъективное мнение экспертов НП «АТС» о том, каким должно быть техническое (не метрологическое!) воплощение АИИС. Все это можно трактовать либо как «вытягивание» показаний приборов в нужную сторону, либо как введение поправки на результат в виде вдруг ставшей известной систематической  погрешности.  В  обоих  случаях такие  операции не имеют ничего общего с метрологией, которая заканчивается там, где получен результат измерений в виде отсчета показаний прибора, доверительных границ случайных  и  неисключенных  систематических  погрешностей и принятой доверительной вероятности. Помимо рассмотренной, но только предполагаемой к внедрению балансировки всего рынка, то есть балансировки «в большом», специалистами  НП «АТС» предлагается  и уже  внедряется  балансировка  «в  малом». Суть ее заключается в манипулировании расчетно-инструментальными операциями при определении значения учетного показателя на сетевом элементе при наличии  средств  измерений  у  обоих  смежных  субъектов рынка. Ситуация показана на рис. 1, 2,  где определению  со  стороны  каждого  субъекта  подлежит значение ∆W на основании измерений  ∆W₁,  ∆W₂, других режимных параметров и расчетов с помощью математической модели сетевого элемента, в качестве которого в большинстве случаев выступает линия электропередачи.

Пусть рассчитанные со стороны 1-го (2-го) субъекта значения учетного показателя  ∆W ′₍₁₎(∆W ′₍₂₎ ) являются функцией вектора режимных параметров в точке 1 (2) X1 _(X2) и вектора параметров схемы замещения Y1_(Y2)

 Очевидно, что

 ввиду наличия погрешностей измерений и используемой математической модели сетевого элемента. Предлагается считать небалансом разность  ∆W′₍₁₎ и  ∆ W ′₍₂₎

 и «разносить» ее на результаты измерений с помощью измерительных  систем  (ИС) субъектов  по  вышеназванному  принципу:  пропорционально  границам  погрешностей и «коэффициентам качества». Использовать оба результата для определения одного значения параметра  ∆W со строгих метрологических позиций в рассматриваемом случае можно, только поставив условием измерительной задачи выполнение  неравноточного  измерения двумя  наблюдателями (первая выборка — со стороны субъекта 1, вторая — со стороны субъекта 2). Каждая из выборок в данном случае состоит из одного измерения. При оценке результата неравноточных измерений и его погрешности учитывается степень доверия к полученным результатам в выборках в виде «весов» (весовых  коэффициентов),  которые устанавливаются пропорционально  некоторым  параметрам  или  экспертным оценкам [1, 3-5]. К параметрам i-ой выборки обычно  относят:  дисперсии  σi  (средние  квадратические погрешности S_i), объемы измерений в выборках и т. д. Известно [1], что, если установлена принадлежность всех выборок одной генеральной совокупности, возможно  определение статистических  параметров этой  генеральной  совокупности  и  установление  границ доверительной  вероятности  по  распределению Стьюдента.  При  обработке  результатов измерений  в большинстве случаев [1, 3-5] принято учитывать в весах результатов измерений только σ_i или их точечные оценки S_i:

 В (11) вместо  σ_i(S_i) допустимо использовать граничные  оценки  средних квадратических  погрешностей результатов измерений

 где множитель t при большом числе измерений n равен квантильному множителю z_p, а при малом n — коэффициенту Стьюдента. Наиболее  вероятное  значение  измеряемой величины ~X₀ по результатам измерений в m выборках ~X_i находится по выражению

 Средняя  квадратическая  погрешность  результата неравноточного измерения определяется как

 Возможны и иные алгоритмы обработки неравноточных измерений: например, приведение их к сериям равноточных измерений и т. д. В последнем случае пользуются оценкой средего квадратического отклонения среднего арифметического значения [1]

 где n — число наблюдений (измерений), x_i — результат  i-го  измерения, — x  —  среднее арифметическое значение измеряемой величины, в качестве которого иногда принимается

~X₀ из (13).

Распространим полученные результаты на конкретные неравноточные измерения учетного показателя согласно рис. 1. Этот случай является предельным, так как имеем всего два наблюдения (n = 2), что соответствует числу  степеней  свободы  в  распределении Стьюдента k = 1. Таким образом, приходится иметь дело с распределением  Коши,  для которого  дисперсия  и  среднее квадратическое отклонение не существуют вследствие того, что определяющий их интеграл расходится. Пусть (см. рис. 1) результаты косвенных измерений ∆W  со стороны субъектов 1, 2 выражаются формулами (8), (9), и им присвоены весовые коэффициенты g₁, g₂ . Тогда (13) будет иметь вид

 Так  как  коэффициент  K_g представляет  собой  отношение  весовых  коэффициентов, при  допущении одинаковости  законов  распределения  погрешностей ИС с обоих концов сетевого элемента не имеет значения, каким образом задавать эти погрешности — с помощью точечных оценок или доверительных интервалов

 где  θ₁,  θ₂ — границы относительных погрешностей ИС 1-го и 2-го субъектов.

Рассмотрим следующие примеры.

Пример  1. Результат  косвенного  измерения  со стороны субъекта 1:  ∆W′₍₁₎= 105 МВт, θ₁= 5%; со стороны субъекта 2:  ∆W′₍₂₎= 110 МВт, θ₂=7 %. В абсолютных  единицах погрешности  косвенных  измерений равны соответственно

 Обозначим через t₁, t₂ коэффициенты, связывающие  средние  квадратические погрешности  и  их  границы в (12) для субъектов 1 и 2. Примем их одинаковыми и равными 1,1: t₁= t₂= t = 1,1.

Определим коэффициент K_g по (17).

 затем — результат неравноточного измерения по (16)

 В  качестве  характеристики  погрешности  вначале найдем S₀ из (14):

 Для n = 2 по справочным данным найдем, что коэффициент Стьюдента при доверительной вероятности P = 0,95t_p = 12,71, и доверительная граница погрешности результата неравноточного измерения будет равна

 или 47,7 % от результата более точного измерения.

Определим  теперь  S₀ по  (15),  приняв,  что ∆~W₀ представляет собой некоторое среднее значение результатов измерений

Переходя  к  доверительным  границам  при  том  же t_p, получим

 или 32,2 % от результата измерения у субъекта 1.

Пример 2. В условиях примера 1 погрешность ИС субъекта 2 увеличилась до 20 % при тех же показаниях прибора. В этом случае θ2= 20 %,

 А значения K_g и ∆~W₀ будут равны

 Переходя  к  доверительным  границам  по  распределению Стьюдента, получим

 что составляет, соответственно, 56,16 % и 40,55 % от результата наиболее точного измерения. На  основании  анализа  формул  (14)-(17)  и  результатов  решения  примеров  1 и  2  можно  сказать следующее.

1. Результат неравноточного измерения смещается в сторону того результата (выборки), погрешность которого меньше.

 2.  Вследствие  квадратичной  зависимости  от  точечных характеристик и границ погрешностей отдельных измерений (выборок) при отличии значений этих величин друг от друга в 4-5 раз результат неравноточного измерения мало отличается от результата более точного измерения (выборки).

3.  Хотя  определенные  по  формуле  (14)  средние квадратические погрешности результата неравноточного измерения всегда меньше, чем средние квадратические погрешности каждого из измерений (каждой выборки),  доверительные  границы погрешности  неравноточного  измерения  резко  возрастают  и  значительно  (в  несколько раз)  превышают  доверительные границы каждого измерения (выборки).

4. Отсюда следует, что нет никаких оснований подвергать неравноточным измерениям физическую величину,  если  количество  составляющих  его  измерений (выборок) мало. В данном случае целесообразно ограничиться  однократным  измерением,  выполненным с наименьшей погрешностью.

 Поэтому в качестве условия измерительной задачи определения значения учетного показателя на сетевом элементе и ей подобных не должно выступать требование выполнения неравноточных измерений, а в  соответствующей  учетной  задаче  не  следует  ссылаться на метрологические причины для попыток балансировки значений этого показателя. При этом никаких иных объективных причин для балансировки не существует.

  ВЫВОДЫ

 1. При создании и функционировании системы коммерческого учета электрической энергии следует  различать  постановку  и  решение  учетных  и измерительных задач. Причем, результаты  решения учетной задачи служат основными условиями измерительной задачи.

2. Средством решения измерительной задачи служат  измерительные,  в  том  числе автоматизированные, системы, а результатом — результаты измерений,  которые  носят принципиально  вероятностный  характер  и  не  допускают  выражения каким-то одним определенным числом.

3. Учетные задачи решаются вне измерительных каналов измерительных систем, зачастую даже вне самих этих систем. Результаты измерений служат исходными данными для решения учетной задачи.  Результаты  решения  учетной  задачи  — только детерминированные числа.

4.  Противоречие  между  требованиями  к оформлению  результатов  решения  учетной  и измерительной задач является источником попыток «исправления» измерительной информации с целью  подгонки  значений  учетных  показателей  для сведения к нулю невязки балансовых уравнений.

5.  Чтобы  придать  видимую  легитимность  искусственному  сведению  небаланса  к нулю  предпринимаются усилия (в том числе и органами государственной метрологической службы) по созданию соответствующих алгоритмов, использующих метрологические характеристики средств измерений (чаще всего — границ погрешностей).

6. Ни теория, ни практика метрологии не дают никаких оснований для исправления результатов измерений в угоду выдуманным принципам балансировки значений учетных показателей в учетной задаче.

7.  Провозглашенный  НП  «АТС»  принцип  балансировки значений учетного показателя на сетевом элементе,  определенных  со  стороны  субъекта  1  и субъекта 2, не имеет под собой ни одной технически объективной  причины,  а  с  метрологической  точки зрения просто бессмыслен, так как приводит к резкому и недопустимому увеличению доверительных границ погрешности полученного результата.

8.  Выход  из  противоречия  между  формой  результатов  решения  измерительной  и учетной  задач заключается во введении в каждое балансовое уравнение учетной задачи специального детерминированного  учетного  показателя  под  названием «неопределенность расчетного баланса».

Его появление — это неустранимое ограничение учетной задачи, операции с которым выходят за ее рамки. Иными словами, в случае оптового рынка электрической  энергии,  учет и  оформление  обязательств  по  оплате  неопределенности  расчетного баланса должны определяться правилами работы рынка,  а  не  корректировкой  «в  нужную  сторону» объективных показаний измерительных систем.

 Автор: Осика Л.К., канд. техн. наук, ЗАО «ЦДР ФОРЭМ»

Материал взя  с сайта 

т

Проблема сбалансированности данных коммерческого учета электроэнергии